Израда сложенијих цртежа помоћу петљи¶
Правилност коју желимо да искористимо на цртежима може да буде и нешто сложенија. Ево неких примера:
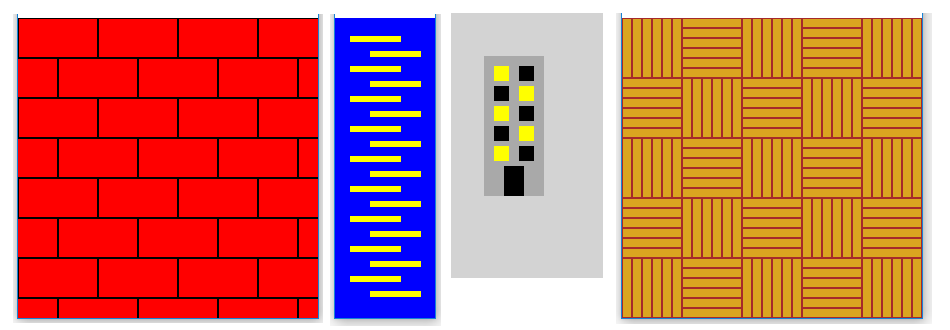
У свим овим случајевима правилност и даље постоји и може да се искористи при писању програма. Осим тога, можемо да приметимо да примери са слике сви имају нешто заједничко, а то је да се наизменично појављјују два правила. На пример, на цртежу са циглама први ред почиње целом циглом, други половином цигле, трећи опет целом и тако даље. Слично томе, на цртежу зграде се наизименично појављују осветљени и затамњени прозори.
Због наизменичног појављивања два правила на цртежима, и програми који их цртају ће имати неких сличности. Погледајмо примере.
Пример - рајсфершлус¶
Да бисмо нацртали овакав рајсфершлус, линије ћемо свакако цртати у петљи. Са цртежа се види да је свака следећа линија за исти број пиксела ниже од претходне, тако да не би требало да буде проблема са рачунањем \(y\) координата. Нешто је тежа ситуација са \(x\) координатама, јер се оне мењају по мало сложенијем правилу.
Овај проблем можемо да решимо помоћу if наредбе у петљи. Након цртања једне линије, проверавамо коју од две могуће вредности има \(x\) координата почетка линије, па ако има прву вредност - додељујемо јој другу и обрнуто. Ево како то изгледа у програму:
Друга могућност да решимо проблем са \(x\) координатама је да у једном проласку кроз петљу цртамо по две линије, на пример овако:
Пример - Цигле¶
Већ смо поменули да редови цигала наизменично почињу целом циглом и половином цигле. Зато при цртању цигала можемо да искористимо исте две идеје као и у претходном примеру.
Нека је дужина цигле означена са \(a\), а њена висина са \(h\). Целу циглу на почетку реда добијамо тако што цртамо правоугаоник од тачке на датој висини, са \(x\) координатом једнаком нули. Половину цигле на почетку реда можемо да добијемо тако што нацртамо целу циглу померену за \(a \over 2\) улево, то јест тако што цртамо правоугаоник од тачке на истој висини, али са \(x\) координатом једнаком -a // 2. Тако постижемо да се види само десна половина цигле. Остаје да решимо када цртамо померену циглу а када не.
Једно решење је да место почетка реда цигала чувамо у променљивој, назовимо је x_poc. После сваког исцртаног реда, проверавамо да ли променљива x_poc има вредност нула или -a // 2. Као и у претходном примеру, коју год од ове две вредности променљива имала, доделићемо јој ону другу вредност, да би у следећем реду цртање цигала почело другачије.
Довршите наредбе за додељивање вредности променљивој x_poc.
Друга идеја је да у сваком проласку кроз двоструку петљу цртрамо циглу коју смо цртали и у првом решењу, а осим ње и циглу испод и полу-лево од ње. Приметите да у том случају петља по y0 има двоструко већи корак, јер унутрашња петља црта два реда цигала.
Довршите наредбе за цртање правоугаоника у овом програму.
Задаци за вежбу¶
Задатак - шаховска табла
Нацртати шаховску таблу преко целог прозора (поља табле треба да буду величине 50х50 пиксела). Доње лево поље треба да буде тамне боје.
Задатак - Зграда
Измените програм тако да се прозори цртају у двострукој петљи.
Део који треба изменити, након измене може да почиње овако:
for y in range(5): # sprat
for x in range(2): # strana zgrade (0 - leva, 1 - desna)
if (x+y) % 2 == 0:
boja = ...
Ако са свим овим задацима нисте имали већих проблема, покушајте за крај да решите и један мало тежи задатак.
Задатак - изазов: Паркет
Напишите програм који приказује паркет (слику паркета можете да видите када кликнете на дугме „Прикажи пример”, а слика је иста као на почетку ове стране, десно). Циљ је, наравно, да се цртање дашчица паркета обавља у вишеструкој петљи. Димензије дашчице су 10х60, а боје су „goldenrod” и „brown”.
Костур програма угрубо изгледа овако:
for red ...
for kol ...
if ...
for dascica in range(6):
pg.draw.rect(...)
else:
for dascica in range(6):
pg.draw.rect(...)
