Криптовање помоћу јавног кључа¶
Природно, први криптосистеми су држали у тајности и сâм поступак криптовања и кључ за енкрипцију и декрипцију. Такви системи су подразумевали да само пошиљалац и прималац поруке знају и поступак енкрипције и декрипције, тј. функцију \(F\), и кључ који се тренутно користи. Овакве системе називамо системима са тајним кључем. Ако се за енкрипцију и декрипцију користи исти кључ, систем је симетричан.
Почетни кључ је могао да буде договорен раније, пре него што се пошиљалац и прималац раздвоје. Као што смо поменули, потенцијални проблем код оваквих криптосистема је што може да буде тешко да се нови кључ касније достави на безбедан начин. Ипак, овакви системи су дуго коришћени са доста успеха. Познат је и обрнути пример из другог светског рата, када је британска обавештајна служба открила систем који су Немци користили за криптовање порука. Након откривања шифре, Британци су успешно пресретали и кључеве коришћене у каснијој комуникацији.
Овакви системи због своје природе нису били погодни за масовну употребу, јер са повећавањем броја корисника било би практично немогуће очувати тајност поступка. Да би неки криптосистем могао да се користи масовно, било је потребно да се осмисли такав начин криптовања у коме ни сâм поступак, а ни кључ за криптовање не би морали да буду тајни (свако може да шаље поруке). Одавде следи да за криптовање и декриптовање морају да се користе различити кључеви. Дакле, трагало се за криптосистемом са следећим особинама:
постоје два различита кључа, један за криптовање, а други за декриптовање
поступак криптовања/декриптовања и кључ за криптовање су јавно доступни
кључ за декриптовање се чува у тајности и познат је само примаоцу порука
поступак генерисања кључева треба да буде рачунски јефтин (да рачунар може брзо да га обави)
поступак криптовања и декриптовања такође треба да буде рачунски јефтин
поступак разбијања шифре (израчунавања кључа за декрипцију) треба да буде рачунски веома скуп, тако да је рачунару за то потребно огромно време.
Суштина је у томе да функција криптовања \(F\) треба да се релативно лако израчунава (кључ за криптовање је свима познат), а да израчунавање њој инверзне функције без познавања кључа за декрипцију захтева тако огромно време, да је практично неизводљиво. Функција са оваквом особином се у рачунарству назива једносмерна функција (енгл. one-way function). Ово не треба мешати са појмом „1-1” (обострано једнозначне) функције, тј. функције која има инверзну функцију.
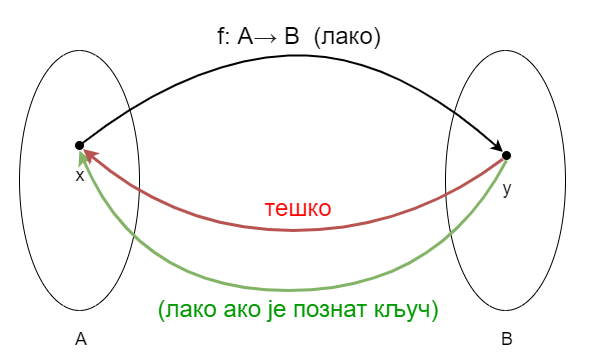
Једносмерна функција¶
Криптовање помоћу јавног кључа је слично закључавању и откључавању сефа са нумеричком комбинацијом. Свако може једноставно да закључа сеф, а откључавање је практично немогуће без познавања комбинације.
Сценарио употребе криптовања помоћу јавног кључа сада можемо сликовито да опишемо на следећи начин. Организатор криптосистема направи велики број оваквих сефова и подели их бесплатно. Свако може да користи сеф тако што стави поруку у њега, закључа сеф и пошаље га организатору система. Ако би неко и пресрео овакву пошиљку, било би му потребно веома много времена да дође до поруке и прочита је. Са друге стране, организатор система зна комбинацију која отвара сеф и лако долази до поруке.
Један систем са овим особинама је осмишљен 1977. године, а у наредним деценијама је постао веома познат и масовно коришћен. Реч је о чувеном алгоритму RSA, који је добио име по иницијалима својих аутора (RSA - Rivest, Shamir, Adleman).
Формално гледано, сваки алгоритам можемо да схватимо као математичку функцију која пресликава улазне податке у излазне. У том смислу, и алгоритам RSA је математичка функција која користи неки кључ \(k\) као параметар, а пресликава улаз \(X\) у излаз \(Y\), то јест \(Y = RSA(k, X) = RSA_k(X)\).
Када неко жели да пошаље поруку \(P\) криптовану овим алгоритмом, треба да примени алгоритам RSA са јавно доступним кључем \(e\) као параметром и тако добије шифрат \(C=F(P)=RSA(e, P)=RSA_e(P)\). Када криптована порука \(C\) стигне до примаоца, он је декриптује истим алгоритмом, али користећи приватни кључ \(d\) који је доступан само њему и добија полазну поруку \(P=F^{-1}(C)=RSA(d, C)=RSA_d(C)\).
Пошто је алгоритам RSA познат и јавно доступан, можда сте помислили да би нападач могао, на основу такође јавно доступног и познатог кључа \(e\), да израчуна приватни кључ \(d\), тако да пресликавање \(RSA_d\) буде инверзно пресликавању \(RSA_e\). Упркос томе што је познат чак и математички поступак израчунавања тајног кључа \(d\), нападач ипак не може да спроведе тај поступак. У наставку можете да прочитате зашто је то тако.

