9.2. Дефинисање функција¶
Видели смо колико је корисно када на располагању имамо дате функције
попут min, max или abs. Сви програмски језици, па и Python
допуштају корисницима да дефинишу своје функције.
У програмима са корњача графиком смо се срели са дефинисањем функција, што нам је омогућило да проширимо језик који корњача разуме и да лакше пишемо програме. Једном када се дефинише функција, практично нема разлике између њеног коришћења и коришћења неке од уграђених наредби, тако да су нам функције заправо омогућиле да дефинишемо нове, сложеније наредбе корњачи. Функције могу да, на основу улазних вредности, израчунају неки резултат и врате га нашем програму, али могу и да промене стање програма и тада не враћају никакав резултат. На пример, abs је функција која на основу дате вредности броја одређује његову апсолутну вредност, док је kvadrat(a) функција која не враћа никакву вредност, већ наређује корњачи да нацрта квадрат на екрану. Функција input, коју смо користили за учитавање са тастатуре, функција је која враћа унету вредност, док је print функција која не враћа никакву вредност, већ мења стање програма, тј. оно што је исписано на екрану.

- Функције су вишеструко корисне приликом програмирања, а издвојићемо следеће:
Функције доприносе томе да наш програм буде краћи и читљивији јер се програмирају на једном месту, а после се само позивају.
Ређе се праве програмске грешке (багови), и лакше се отклањају (дебагују).
Када је потребна измена у функцији, ради се само на једном месту, у наредбама функције.
Функције омогућавају поделу задатака у програмерском тиму, где свако добије одређени део посла, најчешће да испрограмира неке функције, а после се цео програм склапа у целину (функције чине програм модуларним).
Погледај наредни видео:

Примери дефинисања функција¶
На пример, функција која израчунава обим правоугаоника се може дефинисати и онда употребити на следећи начин.
Дефиниција функције почиње речју def, након тога се наводи назив
функције, затим у заградама наведени улазни параметри функције и
симбол двотачка (:). Након те прве линије наводи се тело
функције, које мора бити мало увучено. Код најједноставнијих функција
(као што су ове две наведене у примерима) тело функције представља
само наредба return након које се налази израз који представља
везу између улазних параметара и резултата функције. Код
компликованијих функција у телу се налазе дужа израчунавања, али је наредба
return и даље ту (најчешће на самом крају), a иза ње се наводи вредност функције (то може бити и име
променљиве у којој је израчуната резултујућа вредност). Функције се
позивају тако што се наведе њихов назив и у загради вредности аргумената (параметара).
У претходном примеру, позив функција је гласио obim_pravougaonika(4.2, 5.7), а бројеви 4.2 и 5.7 су у том примеру аргументи (параметри) функције
Површина сложених облика¶
Размотримо проблем израчунавања површине наредних сложених облика.
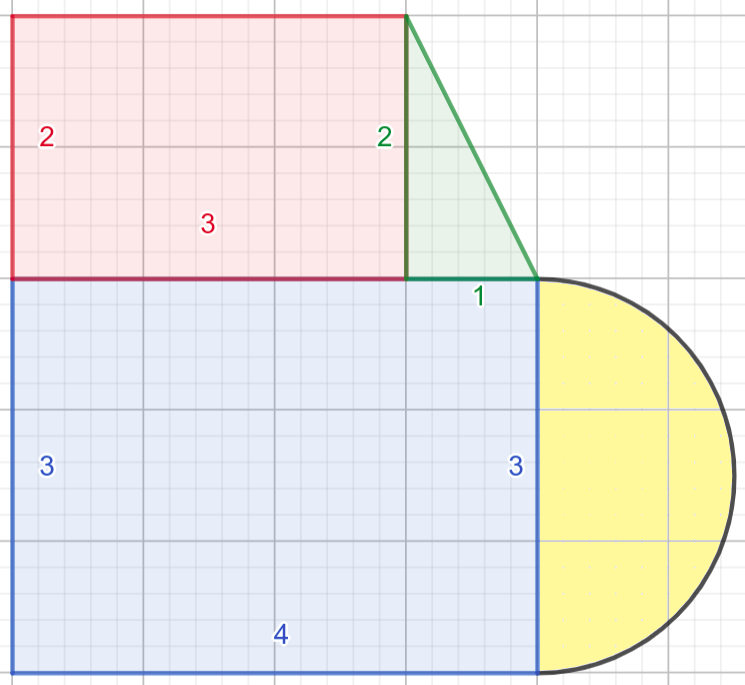
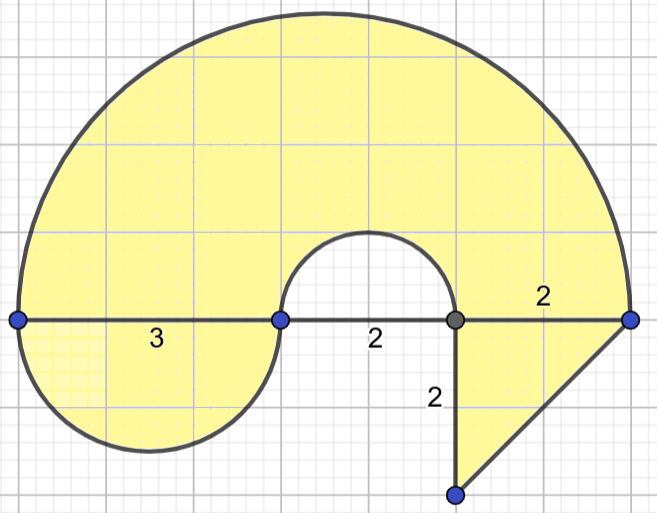
Први облик се може разложити на два правоугаоника, један правоугли троугао и један полукруг, док се површина другог облика може добити тако што се од површине највећег полукруга одузме површина најмањег, а дода површина средњег полукруга и површина правоуглог троугла.
Ако једном дефинишемо функције за израчунавање површине сваког од тих елементарних облика, веома једноставно у главном програму можемо израчунавати површине разних сложених облика, не размишљајући више о формулама потребним за израчунавање површине појединачних облика (површина правоугаоника страница \(a\) и \(b\) израчунава се по формули \(P=a\cdot b\), површина правоуглог троугла чије су странице које образују прав угао \(a\) и \(b\) једнака је \(\frac{a\cdot b}{2}\), јер је тај троугао половина одговарајућег правоугаоника, а површина круга полупречника \(r\) може се израчунати по формули \(P = r^2\pi\), где је \(\pi = 3,1415926...\), а у језику Python се може добити помоћу math.pi).
Функције са више резултата¶
У неким ситуацијама функција треба да врати више вредности. На пример, желимо да претварање центиметара у метре и центиметре опишемо у облику посебне функције. Резултат тада можемо вратити у облику пара или торке елемената (више речи о паровима и торкама је дато у поглављу о представљају података у програмима).
Секунде у сате, минуте и секунде¶

Напиши функцију која на основу броја секунди протеклих од претходне поноћи израчуна тренутно време у сатима, минутима и секундама, водећи рачуна да број сати буде између 0 и 23.
У наредној дефиницији функције направљено је неколико грешака. Исправи је тако да наредни програм да тачне резултате.
Када програм покренеш, треба да испише 0 : 16 : 40 и 2 : 0 : 0.
Сврха дефинисања функција¶
Резимирајмо на крају неколико основних разлога за дефинисање функција.
Увођењем функција добијају се разумљивији програми (ономе ко чита главни програм много је јасније да се у неком делу израчунава обим правоугаоника ако у програму види израз
obim_pravougaonika(2, 5)него ако види израз2 * 2 + 2 * 5)). Када дефинишемо погодне функције, главни програм је много лакше написати.Функције помажу да се програм скрати тако што се избегава понављање истог програмског кода (ако је тај програмски код дугачак и компликован, издвајање у функцију може знатно поједноставити и скратити програм). Ако се покаже да је тај део кода често потребно мењати (што је често случај у програмирању) то што се код јавља само једном (у склопу тела функције) чини одржавање много једноставнијим (не морамо измене да правимо на много места, већ само на једном).
Функције помажу и да се неки проблеми реше, тако што омогућавају разлагање комплексних проблема на једноставније, потпроблеме.