9.4. Вежбање¶

Коришћење уграђених (библиотечких) функција и дефинисање сопствених функција можеш прво провежбати кроз једноставне примере из Збирке малих задатака на следећем линку а затим прећи на задатке који следе.
На крају ти остављамо неколико задатака за вежбу. Оне задатке које не стигнеш да урадиш на часу уради за домаћи задатак.
Време чекања на станици¶

Јелена је дошла аутобусом на станицу у s1 сати и m1 минута, док је Иванин аутобус стигао у s2 сати и m2 минута. Колико је сати и минута она која је прва стигла чекала ону која је друга стигла?
И у овом задатку се тражи да се израчуна растојање између два временска тренутка за које се не зна који је први, а који други. Као што смо приказали раније, рачунање растојања се своди на рачунање апсолутне вредности разлике, а рад са сатима и минутима лакше обављамо ако прво претворимо све у минуте, затим израчунамо број минута колико су се чекале и након тога ту вредност претворимо у сате и минуте.
Менхетн растојање¶

Менхетн, део града Њујорка, организован је у авеније у правцу север-југ и улице у правцу исток-запад. Размак између две улице је 80 m, а између две авеније је 275 m. Ако се Том налази на углу улице \(u_1\) и авеније \(a_1\) и жели да стигне на угао улице \(u_2\) и авеније \(a_2\), колико ће метара морати да пређе.
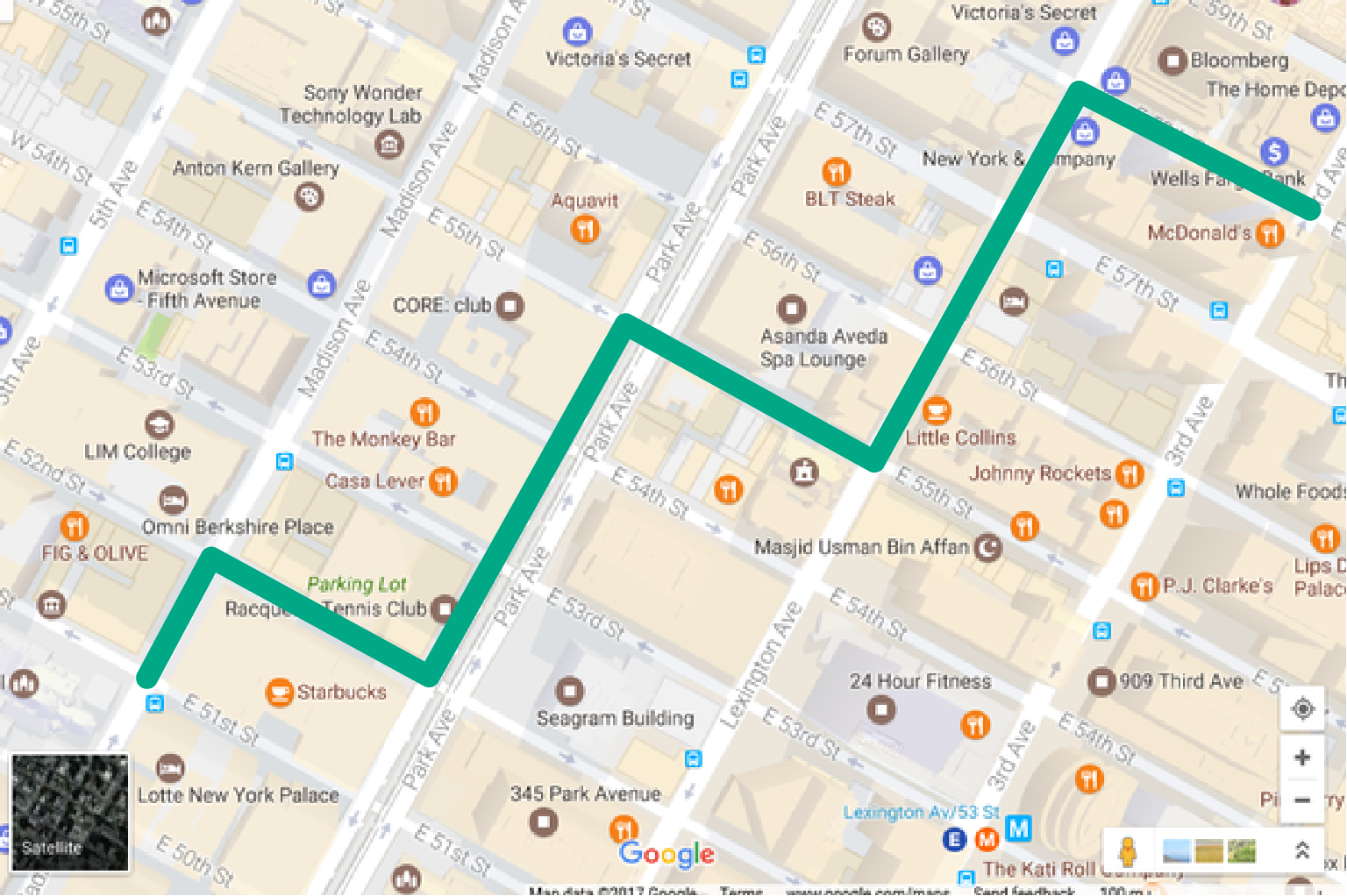
Том има више начина да стигне са једног на друго место (може да иде цик-цак, на разне начине), међутим, пређено растојање је исто као када би прво ишао улицом \(u_1\) све док не дође до угла са авенијом \(a_2\), а затим да се креће авенијом \(а_2\) све док не дође до угла са улицом \(u_2\). Дакле, потребно је израчунати растојање између авенија \(a_1\) и \(a_2\) (да би се оно добило у метрима, потребно је помножити апсолутну разлику између њихових редних бројева размаком између суседних авенија) и на то додати растојање између улица \(u_1\) и \(u_2\) (да би се оно добило у метрима, потребно је помножити апсолутну разлику између њихових редних бројева размаком између суседних улица).
Исправи наредни код тако да коректно израчуна пређени пут (наравно, програм треба да ради и када се улазни подаци промене или учитају са улаза).
Просек три броја¶

Димитрије, Ања, Ивона и Марко су високи редом 165, 162, 158 и 171 cm. Пријављују трочлану екипу за школски турнир у кошарци и у формулару је неопходно да наведу просечну висину своје екипе, али се још нису одлучили ко ће сачињавати екипу. Дефиниши функцију за израчунавање просека три броја, а затим испиши просечне висине за сваку од четири могуће варијанте трочлане екипе.

