9.1. Релативне координате - утврђивање¶

Саобраћајни знак од једнакостраничних троуглова¶

Напиши програм који исцртава саобраћајни знак укрштања са путем са првенством пролаза који је у облику жутог једнакостраничног троугла са црвеном ивицом, окренутог тако да му је хоризонтална основица горе.

Ефекат троугла који је жуте боје и има дебелу црвену ивицу постићи ћемо тако што ћемо нацртати прво већи црвени троугао, а затим мањи жути троугао. Та два троугла ћемо поставити тако да им се тежишта (уједно и све значајне тачке) поклапају и да су исто оријентисани.

Приликом цртања саобраћајног знака потребно је да одредимо поступак којим се црта једнакостранични троугао. Сидро ћемо поставити у тежиште \(T\), које има координате \((t_x, t_y)\). Димензија троугла може бити било дужина странице \(a\), било висина \(h\), јер се из једне од ових димензија друга једноставно израчунава на основу познате везе \(h = \frac{a\sqrt{3}}{2}\).

Извођење везе висине и странице применом Питагорине теореме

Веза \(h = \frac{a\sqrt{3}}{2}\) се лако изводи применом Питагорине теореме на правоугли троугао чија је једна катета висина једнакостраничног троугла, друга половина странице, а хипотенуза је страница једнакостраничног троугла.

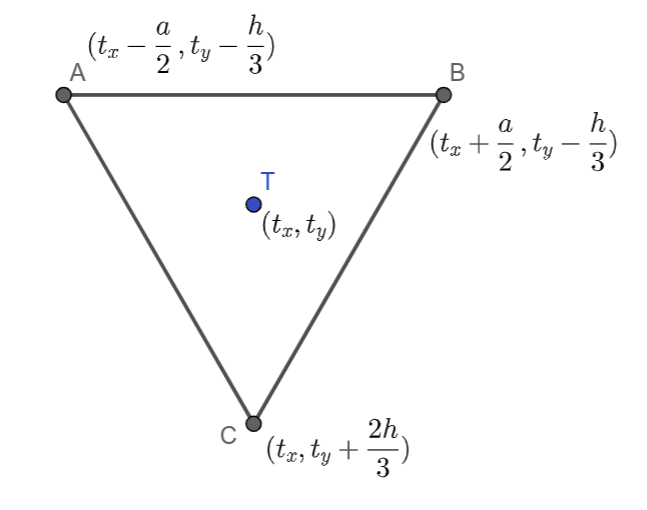
Из математике знамо да тежиште троугла дели тежишну дуж (у овом случају то је уједно и висина) у односу \(2:1\), тако да су координате темена \(A\) и \(B\) у односу на ову тачку померене (транслиране) на горе за \(\frac{1}{3}h\), док је тачка \(C\) померена на доле за \(\frac{2}{3}h\).

Координате \(x\) ових тачака одређујемо у односу на тачку \(T\), користећи дужину странице \(a\). Тачка \(А\) је померена од тежишта за \(\frac{а}{2}\) ка левој ивици прозора. Тачка \(В\) је померена од тежишта за \(\frac{а}{2}\) ка десној ивици. Тачка \(C\) има исту \(x\) координату као и тежиште.

Дакле, тачка \(A\) има координате \((t_x-\frac{a}{2}, t_y-\frac{h}{3})\), тачка \(B\) има координате \((t_x+\frac{a}{2}, t_y-\frac{h}{3})\), док тачка \(C\) има координате \((t_x, t_y+\frac{2h}{3})\).

Пошто је потребно да нацртамо два троугла, можемо дефинисати функцију за цртање троугла и позвати је два пута (за исто тежиште, али различите боје и димензије). Тежиште ћемо поставити хоризонтално на средину прозора, док ћемо га вертикално поставити тако да троугао делује центриран по средини прозора. Оставићемо простор (маргину) од по 30 пиксела изнад и испод троугла, а тежиште троугла ћемо поставити тако да преосталу висину дели у односу 1:2.

На основу претходне дискусије допуни наредни програм:

Цвет¶

Напиши програм који исцртава цвет који се састоји од централног жутог круга пречника 100 пиксела, око којег се налази 6 правилно распоређених латица розе боје, свака у облику круга, такође пречника 100 пиксела (центри латица се налазе у теменима правилног шестоугла, чији је центар у центру цвета, а дужина странице је 100 пиксела).

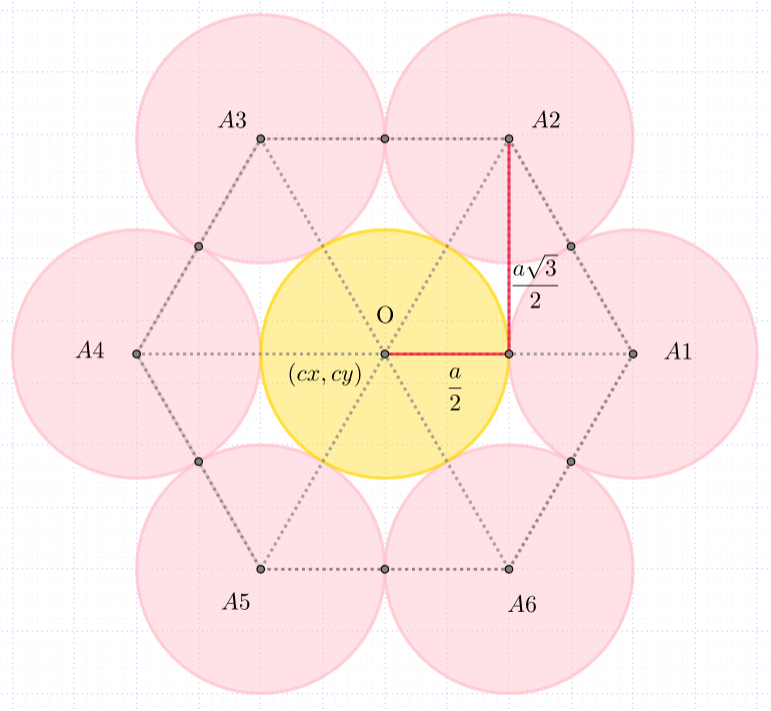
За цртање круга потребно је знати координате центра и дужину полупречника круга. Пречник свих кругова је једнак, самим тим и полупречник \(r = \frac{a}{2}\). Нека је тачка О центар жутог, централног круга. Координате ове тачке означимо са \((c_x, c_y)\). Ова тачка се налази у центру прозора и њене координате једнаке су половини висине, односно ширине прозора. Координате осталих центара кругова изразићемо такође преко координата \((c_x, c_y)\). Координате тачке \(А_1\) означимо са \((x_1, y_1)\). Тачка \(А_1\) је за \(a\) померена (транслирана) од тачке О по оси \(x\), тако да је \(x_1\), прва координата ове тачке једнака \(x_1 = c_x + a\), а друга координата ове тачке \(y_1\) једнака је \(y\) координати тачке О, тј. \(y_1 = c_y\). Координате тачке \(А_2\) означимо са \((x_2, y_2)\). Ова тачка је у односу на тачку О померена (транслирана) за \(\frac{a}{2}\) по оси \(x\), односно за висину \(h = \frac{a \sqrt{3}}{2}\) једнакостраничног троугла \(\triangle OA_1A_2\) по оси y. На основу овога закључујемо да су координате тачке \(А_2\) \((x_2, y_2) = (c_x+\frac{a}{2}, c_y + h)\). Координате центра осталих кругова одређујемо на сличан начин.

На основу претходне дискусије, допуни наредни програм и поправи грешке везане за тип података бројева: