Просек и медијана низа бројева¶

Просек низа¶

Постоји много ситуација када се низ бројева може згодно описати неком карактеристичном вредношћу. На пример, ученици добијају оцене из много предмета, али на крају школске године школски систем жели да „изведе” једну оцену и да том оценом окарактерише рад ученика у тој години.

Временом се као један од погодних представника низа бројева показао просек. Просек низа бројева се рачуна овако:

Дакле, да бисмо добили просек низа бројева саберемо све елементе низа и тако добијени број поделимо дужином низа.

У Пајтону се обе ове активности могу обавити позивом одговарајуће уграђене функције: функција len рачуна дужину низа, док функција sum рачуна збир елемената низа бројева.

На пример:

In [1]: L = [1, 3, 5, 7, 9, 10]
   ...: print(len(L))
   ...: print(sum(L))
   ...: 
6
35

(Примети да су ове функције уграђене у Пајтон и да нема потребе ловити их по библиотекама!)

Према томе, просек низа бројева се у Пајтону рачуна овако:

In [2]: print("Prosek niza brojeva", L, "je", sum(L) / len(L))
Prosek niza brojeva [1, 3, 5, 7, 9, 10] je 5.833333333333333

Како ћемо у много наврата рачунати просек, дефинисаћемо нову функцију која га рачуна. У претходним разредима смо се већ срели са дефиницијама нових функција у Пајтону и зато мали програм који следи не би требало да представља изненађење за тебе:

In [3]: def prosek(L):
   ...:     return sum(L) / len(L)
   ...: 

Претходни програм је у систем унео нову дефиницију: функција prosek ће прихватити неки низ L и онда ће као резултат свог рада вратити збир елемената низа L подељен дужином низа L (дакле, просек елемената тог низа).

Примети да је списак Пајтон наредби које представљају тело функције и објашњавају шта функција ради увучен за четири празнине.

Да видимо како ради наша нова функција:

In [4]: print("Prosek niza brojeva", L, "je", prosek(L))
Prosek niza brojeva [1, 3, 5, 7, 9, 10] je 5.833333333333333

У ћелији испод унете су оцене једног ученика из информатике и приказан је њихов просек:

In [5]: ocene = [5, 3, 5, 4, 4, 5]
   ...: print("Prosek ocena iz informatike je", prosek(ocene))
   ...: 
Prosek ocena iz informatike je 4.333333333333333

Ако ћемо искрено, просек оцена се увек приказује заокружен на две децимале. У Пајтону постоји уграђена функција round(x, n) која заокружује дати број x на n децимала. На пример:

In [6]: round(1.666666666, 2)
Out[6]: 1.67

Према томе, просек оцена из информатике сада можемо да добијемо овако:

In [7]: print("Prosek ocena iz informatike je", round(prosek(ocene), 2))
Prosek ocena iz informatike je 4.33

Сортирање низа и медијана¶

Сортирати низ значи испремештати његове елементе тако да буду поређани по величини, од мањих ка већим или обрнуто. На пример:

Уграђена функција sort сортира низ и позива се овако:

In [8]: L = [3, 1, 2, 5, 0, -1, 4]
   ...: L.sort()
   ...: 

Ако проверимо вредност променљиве L након позива функције sort видећемо да су елементи листе сада поређани од мањих ка већим вредностима:

In [9]: L
Out[9]: [-1, 0, 1, 2, 3, 4, 5]

Ако желимо да поређамо елементе листе L од већих ка мањим вредностима, то можемо да урадимо овако:

In [10]: L.sort(reverse=True)
   ....: L
   ....: 
Out[10]: [5, 4, 3, 2, 1, 0, -1]

Опција reverse=True каже функцији sort да желимо да сортирамо елементе листе у „обрнутом” поретку: од већих ка мањим вредностима.

Ако су подаци са којима радимо „јако разбацани” и „имају велика одступања” може се десити да просек низа није добар представник целог низа. Зато се као друга карактеристична вредност низа често користи медијана. Медијана низа је елемент „на средини сортираног низа” и одређује се овако:

• ако је дужина низа непарна медијана низа је елемент који је тачно на средини низа;

• ако је дужина низа парна медијана низа је аритметичка средина два елемента на средини низа.

На пример, медијана низа [1, 4, 9, 12, 45, 101, 256] је 12

[1, 4, 9, 12, 45, 101, 256]
          ^^
          елемент на средини сортираног низа

док је медијана низа [1, 4, 9, 12, 45, 101, 256, 317] једнака са \(\frac{12 + 45}{2} = 28,5\)

[1, 4, 9, 12,    45, 101, 256, 317]
              ^^
              број на средини између 12 и 45, што је 28,5

Дакле, ако је дужина низа непарна медијана тог низа је његов елемент низа, док у случају да је дужина низа парна медијана је број који не мора бити елемент низа. То може да представља непријатност у неким ситуацијама, па ћемо ми зато у овом курсу користити сродан појам појам који се зове доња медијана низа.

Доња медијана низа је елемент низа који се одређује овако:

• ако је дужина низа непарна, доња медијана низа је број на средини сортиране верзије тог низа (исто као код медијане);

• ако је дужина низа парна, доња медијана низа је мањи од два средишња елемента у сортираној верзији низа.

На пример, доња медијана низа [1, 4, 9, 12, 45, 101, 256] је 12

[1, 4, 9, 12, 45, 101, 256]
          ^^
          елемент на средини сортираног низа

док је доња медијана низа [1, 4, 9, 12, 45, 101, 256, 317] поново 12:

[1, 4, 9, 12, 45, 101, 256, 317]
          ^^  ^^
          мањи од два средишња броја, што је 12

Доња медијана низа се веома лако рачуна:

In [11]: def donja_medijana(L):
   ....:     n = len(L)
   ....:     L.sort()
   ....:     return L[n//2]
   ....: 

У многим ситуацијама (доња) медијана боље представља „средњу вредност“ низа него аритметичка средина низа. Ево примера.

У листи zarade дате су месечне зараде запослених у једној малој приватној компанији исказане у америчким доларима.

In [12]: zarade = [647, 570, 587, 576, 646, 519, 585, 686, 644, 604, 95611, 609, 603, 536, 532, 535, 423180, 619, 600, 624, 545, 582, 890234, 672, 699, 549, 571, 688, 542, 691, 533, 670, 603, 583, 670, 550, 544, 579, 505, 673, 631, 695, 577, 653, 514, 556, 651, 530, 664, 559, 630, 699, 506, 696, 653, 674, 636, 618]

Просечна зарада у компанији је:

In [13]: prosek(zarade)
Out[13]: 24867.896551724138

Међутим, доња медијана овог низа је:

In [14]: donja_medijana(zarade)
Out[14]: 609

Дакле, просечна зарада у компанији је скоро 25.000 америчких долара, али доња медијана свих зарада је 609 америчких долара. То значи да половина запослених у тој компанији има зараду која износи 609 америчких долара или мање. Како је то могуће?

Да бисмо схватили шта се десило, морамо да извршимо детаљнију анализу.

Филтрирање података¶

Филтрирати податке значи из датог низа података издвојити оне који су нам на неки начин интересантни.

Да бисмо схватили како је могуће да је у претходном примеру просечна зарада шест пута већа од медијалне, филтрираћемо натпросечне зараде. Филтрирање листе у Пајтону се може постићи конструкцијом која изгледа овако:

[x for x in Lista if Uslov(x)]

Ова конструкција у нову листу покупи све елементе x листе Lista који испуњавају Uslov. То је као кад у математици напишемо:

Нама су у претходном примеру интересантне зараде које су изнад просека. Да бисмо видели колико их има и које су то зараде прво ћемо просечну зараду сместити у променљиву и онда ћемо филтрирати листу zarade:

In [15]: prosecna_zarada = prosek(zarade)
   ....: natprosecne_zarade = [x for x in zarade if x >= prosecna_zarada]
   ....: 

Натпросечне зараде су:

In [16]: natprosecne_zarade
Out[16]: [95611, 423180, 890234]

и видимо да их има свега

In [17]: len(natprosecne_zarade)
Out[17]: 3

Дакле, у овој компанији троје запослених има огромне зараде, док сви остали имају зараде које су испод просека. Ове три несразмерно велике зараде повећавају просек и дају утисак да „просечна зарада у овој кокмпанији и није толико лоша”, иако је стварно стање знатно другачије.

Ситуације у којима се медијана јако разликује од просека нам говоре да су подаци изузетно неравномерни и да је потребно уложити додатни напор да би се схватило какво стање они описују.

Приказивање података, њиховог просека и њихове медијане¶

Један начин да видимо однос просека и медијане и како они представљају податке је да ситуацију визуелизујемо.

Кренимо од једног једноставног примера. Претпоставимо да је на полугодишту један ученик имао следеће оцене из наведених предмета:

Податке можемо представити помоћу две листе, овако:

In [18]: predmeti = ["mat", "srp", "lik", "ist", "fiz", "muz", "tio"]
   ....: ocene    = [2,     4,     5,     3,     5,     4,     5    ]
   ....: 

Желимо да прикажемо његове оцене хистограмом и да просечна оцена буде означена црвеном линијом како бисмо могли да видимо које оцене су изнад просека, а које испод.

Прво ћемо учитати библиотеку за цртање графикона:

In [19]: import matplotlib.pyplot as plt

Хистограм са оценама можемо да нацртамо веома једноставно:

In [20]: plt.figure(figsize=(10,5))
   ....: plt.bar(predmeti, ocene)
   ....: plt.title("Ocene na polugodistu")
   ....: plt.show()
   ....: 

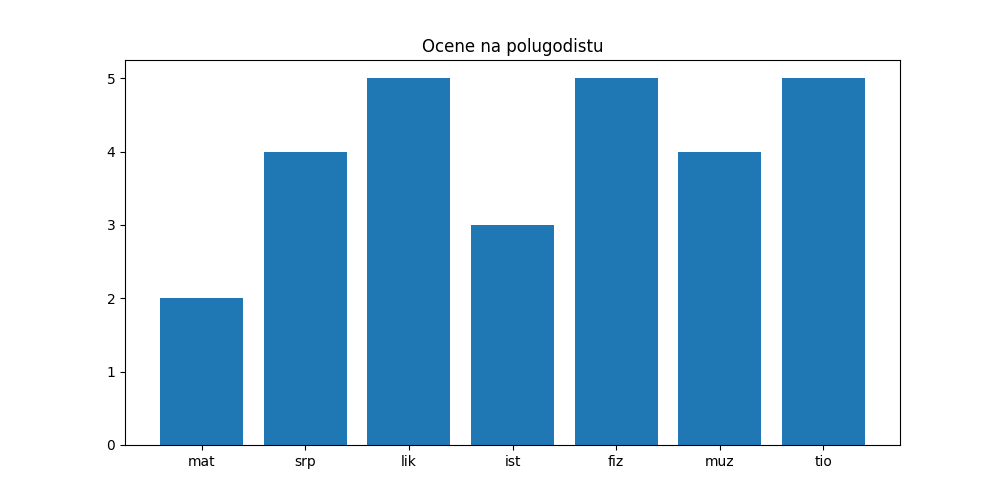
Сада желимо да преко хистограма нацртамо црвену линију која представља просечну оцену. Прво ћемо израчунати просечну оцену po:

In [21]: po = prosek(ocene)

а онда ћемо на горњи дијаграм додати и низ података који изгледа овако:

[po, po, po, po, po, po, po]

In [22]: plt.figure(figsize=(10,5))
   ....: plt.bar(predmeti, ocene)
   ....: plt.plot(predmeti, [po, po, po, po, po, po, po], color="r")
   ....: plt.title("Ocene na polugodistu")
   ....: plt.show()
   ....: 

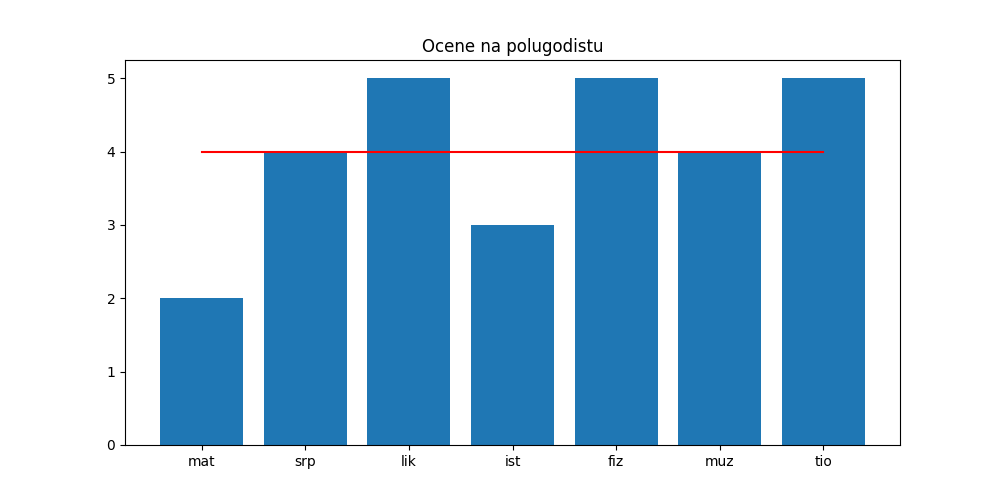
Ако један исти податак s треба поновити n пута можемо да пишемо као горе:

[s, s, s, (и тако даље)]

али можемо да то запишемо краће овако:

[s]*n

Ознаком [s]*n смо Пајтону рекли да желимо да направимо нови низ који се добија тако што се низ [s] „умножи” n пута. На пример, [5]*7 = [5, 5, 5, 5, 5, 5, 5]. (Такође је [6, 7, 8]*3 = [6, 7, 8, 6, 7, 8, 6, 7, 8], али нам ово за сада неће бити потребно.)

Тако добијамо следећу верзију програма:

In [23]: plt.figure(figsize=(10,5))
   ....: plt.bar(predmeti, ocene)
   ....: plt.plot(predmeti, [po] * len(ocene), color="r")
   ....: plt.title("Ocene na polugodistu")
   ....: plt.show()
   ....: 

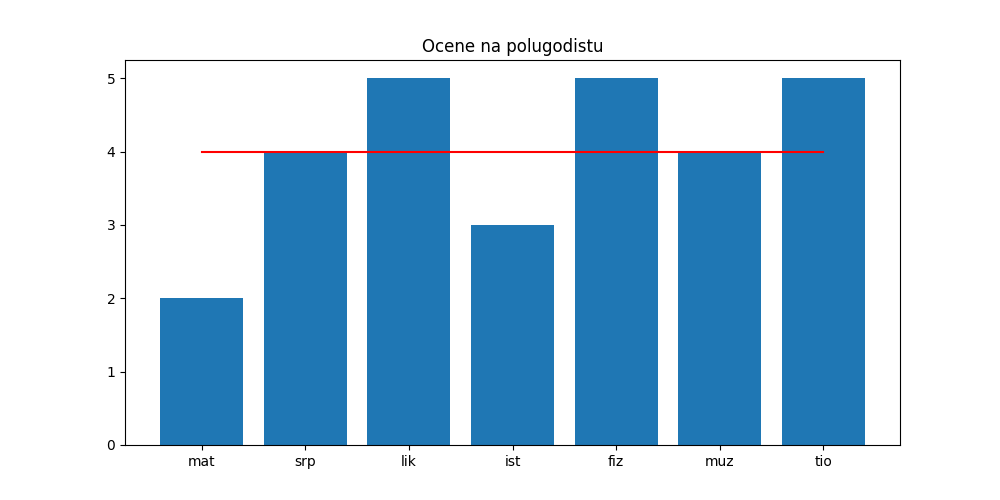
За крај ћемо дијаграму додати легенду:

In [24]: plt.figure(figsize=(10,5))
   ....: plt.bar(predmeti, ocene, label="ocene")
   ....: plt.plot(predmeti, [po] * len(ocene), color="r", label="prosek")
   ....: plt.title("Ocene na polugodistu")
   ....: plt.legend()
   ....: plt.show()
   ....: 

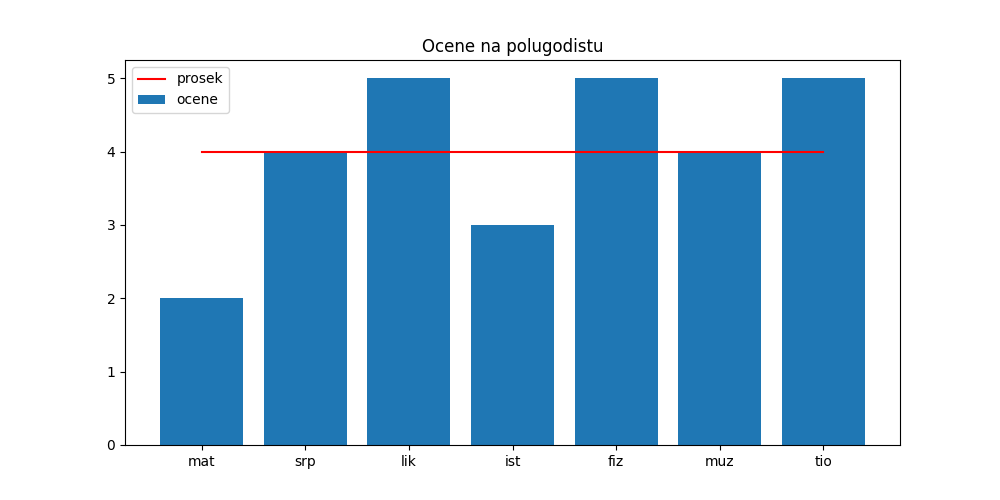
Ево и кратког видеа који илуструје оно што смо до сада видели:

Сада ћемо да визуелизујемо зараде у компанији о којој смо говорили у претходним одељцима.

In [25]: n = len(zarade)
   ....: plt.bar(range(n), zarade)
   ....: plt.show()
   ....: 

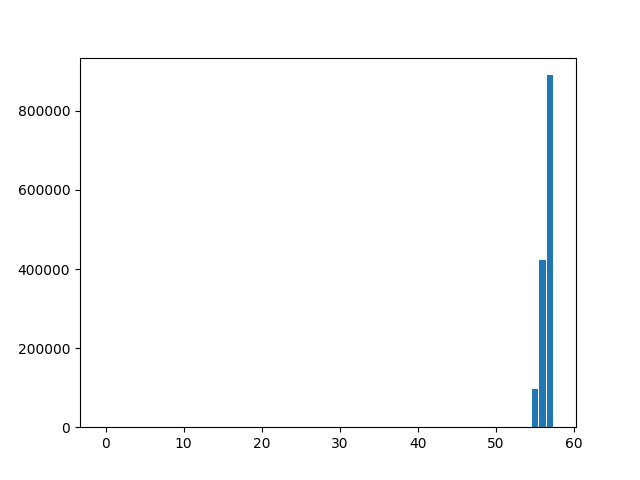
Дакле, ништа се не види.

Мораћемо да повећамо дијаграм и да прибегнемо још једном лукавству. Пошто ми већ знамо да је просечна зарада око 25.000 америчких долара и да има само троје запослених у тој компанији који примају толико или више, ограничићемо вредности које се приказују на \(y\)-оси. Одмах ћемо приказати и просек црвеном линијом.

In [26]: n = len(zarade)
   ....: plt.figure(figsize=(15,5))
   ....: plt.bar(range(n), zarade, color="b")
   ....: plt.plot([0, n-1], [prosecna_zarada, prosecna_zarada], color="r")
   ....: plt.ylim(0,30000)
   ....: plt.show()
   ....: 

На овом дијаграму се јасно види како су несразмерно велике зараде неколицине запослених „повукле просек за собом”.

Погледајмо сада где је доња медијана. Њу ћемо представити као дијаграм са само једним црвеним стубићем на средини низа.

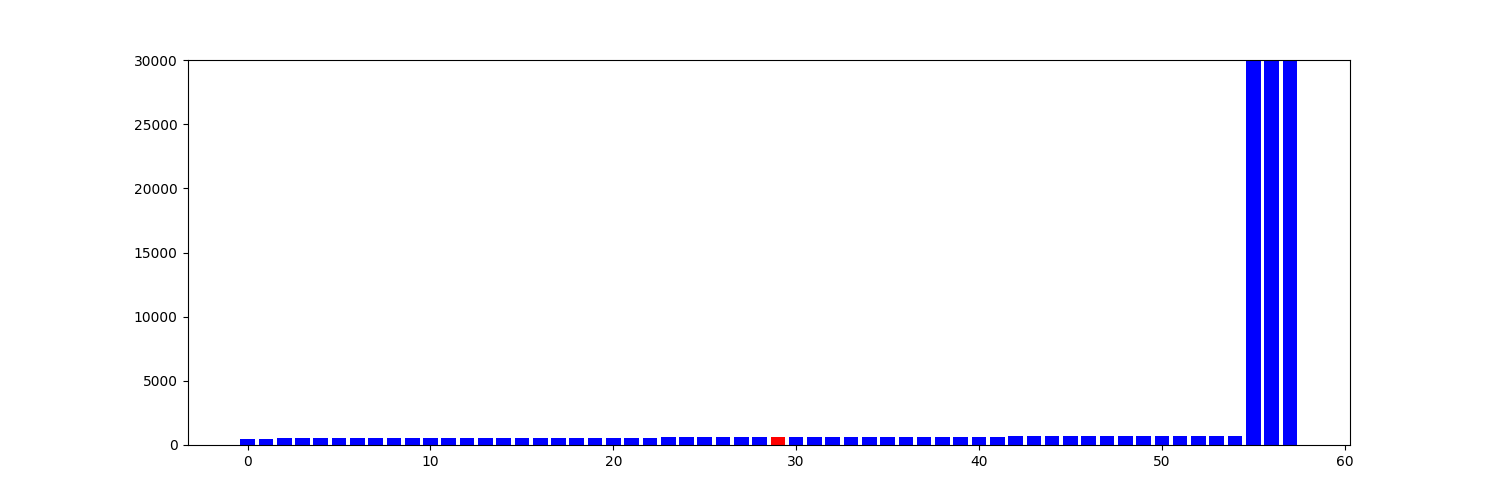
In [27]: n = len(zarade)
   ....: plt.figure(figsize=(15,5))
   ....: plt.bar(range(n), zarade, color="b")
   ....: plt.bar([n//2], [zarade[n//2]], color="r")
   ....: plt.ylim(0,30000)
   ....: plt.show()
   ....: 

Задаци¶

За вежбу покрени Џупитер окружење и реши задатке из радне свеске J04.ipynb