Алгебарски типови података¶

Бинарно дрво¶

Циљ нам је да направимо структуру података којом можемо да представљамо скупове елемената тако да ефикасно можемо да убацујемо нове елементе и да проверавамо да ли елементи припадају скупу. Једна погодна структура података за представљање скупа је бинарно дрво. Бинарно дрво је рекурзивна структура података која се састоји од чворова. У чвору је уписана нека вредност (претпоставићемо, једноставности ради, да је у питању вредност типа Int), а лево и десно се налазе мања дрвета. Излаз из ове рекурзије представља празно дрво које нема ни вредност ни наследнике. Тип података за представљање дрвета може бити дефинисан на следећи начин:

data Tree =
   Empty |
   Node Tree Int Tree

Дрво је, дакле, или празно (Empty) или је у питању чвор који садржи три податка: лево поддрво, вредност типа int и десно поддрво.

Сада можемо да формирамо изразе чији је тип Tree. На пример

Node (Node Empty 2 Empty) 3 (Node Empty 5 (Node Empty 7 Empty))

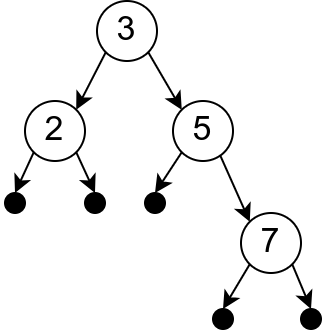
Нажалост, приликом њиховог уноса у интерпретатор добићемо поруку да систем не уме да прикаже дрво. Најједноставнији начин да се то реши је да се аутоматски генерише функција за приказ дрвета, што се постиже тиме што се након дефиниције типа дода deriving Show.

data Tree =
   Empty |
   Node Tree Int Tree
   deriving Show

На овај начин је аутоматски дефинисана функција show :: Tree -> String која на основу датог дрвета гради ниску карактера која представља дрво у истом формату у ком се оно може задати у програму (нпр. Node Empty 2 Empty).

Show је заправо класа типова која садржи типове за које постоји функција show која може да претвори податак тог типа у ниску. Клаузулом deriving Show поред аутоматског генерисања функције show се истовремено наглашава да ће дефинисани тип података припадати класи show. Ми се нећемо детаљније бавити класама типова. Покушај на интернету да пронађеш више информација о овој теми.

Приказани запис дрвета је релативно компликован. Једноставније би било да, на пример, претходно дрво представимо ниском (.2.)3(.5(.7.)) и да дефинишемо функцију parseTree која од такве ниске гради дрво. Употребићемо технику рекурзивног спуста, коју сте срели у првом разреду. Користимо следећу контекстно-слободну граматику.

Пошто су изрази потпуно заграђени, на основу првог карактера одређујемо да ли се примењује прво или друго правило. У другом правилу прво треба да прескочимо отворену заграду, затим рекурзивно да прочитамо лево поддрво, затим да прочитамо број, па да рекурзивно прочитамо десно поддрво и да на крају прочитамо десну заграду. Сваки позив функције парсирања треба да прочита садржај са почетка и да врати прочитано дрво, али и преостали део ниске, иза прочитаног садржаја. Стога дефинишемо помоћну функцију parseTree' која то ради, док главна функција враћа само дрво, занемаривши преостали садржај ниске (ако је ниска исправна, преостали садржај ће бити празан). Наредна имплементација претпоставља да је ниска која се парсира увек исправно задата.

import Data.Char (isDigit)

parseTree :: String -> Tree
parseTree str = fst (parseTree' str)
  where
    parseTree' :: String -> (Tree, String)
    parseTree' str =
      if head str == '.' then
        (Empty, tail str)
      else
        let str1 = tail str;                       -- skip (
            (left, str2) = parseTree' str1         -- read left subtree
            (valueStr, str3) = span isDigit str2   -- read value
            (right, str4) = parseTree' str3        -- read right subtree
            str5 = tail str4                       -- skip )
        in (Node left (read valueStr) right, str5)

Обратимо пажњу на примену функције span isDigit. Функција isDigit :: Char -> Bool је увезена из библиотеке Data.Char (зато је на почетку програма морала бити наведена декларација import) и проверава да ли је дати карактер цифра. Функција span :: (a -> Bool) -> [a] -> ([a], [a]) дели листу на два дела: елементе са почетка листе који задовољавају услов дат као аргумент функције span и остатак листе. Функција read чита бројевну вредност из ниске која представља исправан запис броја.

За представљање скупа ми ћемо користити уређена тј. претраживачка дрвета (енг. binary search tree). Њихова основна особина је да сваки чвор задовољава да се у левом поддрвету налазе вредности које су мање или једнаке од вредности у том чвору, а у десном поддрвету вредности које су веће или једнаке од вредности у том чвору. Ако не желимо дупликате (а скуп обично не садржи дупликате), онда захтевамо да важе стриктне неједнакости (лево су строго мањи, а десно строго већи елементи од оног уписаног у чвору). На основу овога можемо дефинисати рекурзивну функцију за уметање елемента у дрво. Она прима дрво и вредност која се умеће и враћа ново дрво. Приметимо да се већи део полазног дрвета задржава, тако да овај приступ није меморијски превише захтеван (пошто се у функционалном програмирању обично не врши модификација података, они могу бити дељени, без копирања).

Уметање вредности у право дрво даје дрво коме је та вредност у корену, а лево и десно су празна поддрвета. Уметање у непразно дрво подразумева поређење вредности x, која се умеће, са вредношћу уписаном у корен дрвета. Ако је x мање од корена, врши се рекурзивно убацивање у лево поддрво (вредност у корену и десно поддрво остају неизмењени); ако је веће врши се рекурзивно убацивање у десно поддрво (вредност у корену и лево поддрво остају неизмењени), а ако је једнако вредности у корену, онда се цело дрво враћа неизмењено (не желимо да убацујемо дупликате).

insert :: Tree -> Int -> Tree
insert Empty x = Node Empty x Empty
insert (Node left root right) x
   | x < root  =  Node (insert left x) root right
   | x > root  =  Node left root (insert right x)
   | otherwise =  Node left root right

Понављањем ове функције лако можемо да формирамо дрво од листе бројева. Тај поступак можемо имплементирати кроз функцију која формира дрво од елемената листе.

treeOfList :: [Int] -> Tree
treeOfList = foldl insert Empty

Сложеност функције insert и treeOfList зависи од распореда чворова дрвета. У најгорем случају, када је листа од које се формира дрво сортирана, сви чворови ће завршити на једној страни (увек ће лево или ће увек десно поддрво бити празно, у зависности од тога како је листа сортирана). Тада је сложеност функције insert линеарна, а функције treeOfList квадратна. Ипак, ако су елементи који се убацују у дрво насумични, можемо очекивати да ће дрво бити прилично балансирано (да ће број чворова са леве и са десне стране сваког чвора бити отприлике једнак) и тада ће висина дрвета логаритамски зависити од броја чворова дрвета, па ће сложеност функције insert бити \(O(\log n)\), а сложеност функције treeOfList бити \(O(n \log n)\).

Уместо обичних претраживачких дрвета могуће је користити и тзв. самобалансирајућа дрвета. Најпознатије врсте таквих дрвета су АВЛ дрвета и Црвено-црна дрвета. Алгоритам уметања у ова дрвета је такав да се приликом уметања проверава да ли је нарушена равнотежа између левог и десног дела и ако јесте, дрво се ротира тако да би се та равнотежа поново успоставила.

Када је формирано дрво, тада можемо вршити његову претрагу, тј. можемо имплементирати функцију која проверава да ли дрво садржи дати елемент. Празно дрво не садржи ниједан елемент. Непразно дрво претражујемо тако што елемент који тражимо поредимо са вредношћу у корену. Ако је вредност мања од корена, тражимо је рекурзивно у левом поддрвету, ако је већа, у десном, а ако је једнака вредности у корену, онда знамо да дрво садржи тражену вредност.

contains :: Tree -> Int -> Bool
contains Empty x = False
contains (Node left root right) x
  | x < root    = contains left x
  | x > root    = contains right x
  | otherwise   = True

Ово је вероватно добар тренутак да упоредимо приказано решење у језику Haskell са решењем у традиционалном императивном програмском језику, какав је C.

#include <stdio.h>
#include <stdlib.h>

struct Node {
   int value;
   struct Node *left, *right;
};

Node* newNode(int value) {
      Node* new = (Node*)malloc(sizeof(Node));
      new->value = value;
      new->left = new->rigth = NULL;
}

void freeNode(Node* node) {
   if (node != NULL) {
      freeNode(node->left);
      freeNode(node->right);
      free(node);
   }
}

Node* insert(Node* root, int value) {
   if (root == NULL)
      return newNode(value);
   if (value < root->value)
      root->left == insert(root->left, value);
   else if (value > root->value)
      root->right = insert(root->right, value);
   return root;
}

int contains(Node* root, int value) {
   if (root == NULL)
      return 0;
   if (value < root->value)
      return contains(root->left, value);
   else if (value > root->value)
      return contains(root->right, value);
   else
      return 1;
}

Node* treeOfArray(int[] a, int n) {
    Node* root = NULL;
    for (int i = 0; i < n; i++)
       root = insert(root, a[i]);
    return root;
}

void printTree(Node* root) {
   if (root != NULL) {
       printTree(root->left)
       printf("%d ", root->value);
       printTree(root->right);
   }
}

int main() {
    int a = {1, 3, 2, 5, 4};
    int n = sizeof(a) / sizeof(int);
    Node* root = treeOfArray(a, n);
    printTree(root);
    freeNode(root);
}

Примећујемо да су алгоритми који се користе исти као у одговарајућим Hakell функцијама, али да је кôд оптерећен многим техничким детаљима о којима није било потребе водити рачуна у Haskell имплементацији. На пример, у језику C је било потребно ручно алоцирати и ослобађати меморију (коришћењем библиотечких функција malloc и free). Употреба показивача је експлицитна, што на многим местима чини да је кôд оптерећен додатним симболима (попут *, ->) и програм је теже и писати и разумети. Захваљујући библиотечкој функцији fold, имплементација креирања дрвета од листе је много краћа и једноставнија од имплементације у C-у која мора да користи петљу и да ручно имплементира функционалност коју нам пружа fold.

У уређеном дрвету је лако пронаћи минимални и максимални елемент (они се налазе у крајњем левом и крајњем десном чвору).

minTree :: Tree -> Int
minTree (Node Empty x _) = x
minTree (Node left x _ ) = minTree left

Дефинишимо и функцију која уклања тај најмањи елемент дрвета (под претпоставком да је дрво непразно). Функција враћа уређени пар, који се састоји од уклоњене вредности и измењеног дрвета. Ако не постоји лево поддрво корен дрвета је најмањи елемент, а његовим брисањем остаје само десно поддрво. У супротном бришемо најмањи елемент левог поддрвета.

deleteMin :: Tree -> (Int, Tree)
deleteMin (Node Empty x right) = (x, right)
deleteMin (Node left x right)  = let (m, left') = deleteMin left
                                  in (m, Node left' x right)

Ова се функција може искористити и за уклањање дате вредности из скупа (тј. дрвета). Брисањем било чега из празног дрвета дрво остаје празно. Ако је дрво непразно, а вредност која се брише мања од корена, рекурзивно се та вредност брише из левог поддрвета. Ако је вредност већа од корена, рекурзивно се та вредност брише из десног поддрвета. Најкомпликованији је случај када је вредност која се брише једнака вредности у корену. Ако је тада десно поддрво празно, можемо само вратити лево поддрво. У супротном можемо обрисати најмању вредност из десног поддрвета и њу ставити на место корена (аналогно бисмо могли обрисати највећу вредност из левог поддрвета и њу ставити на место корена). Да бисмо анализирали да ли је десно поддрво празно или непразно, можемо употребити израз case-of.

delete :: Int -> Tree -> Tree
delete _ Empty = Empty
delete x' (Node left x right)
   | x' < x      = Node (delete x' left) x right
   | x' > x      = Node left x (delete x' right)
   | otherwise   = case r of Empty -> left
                             _     -> let (m, right') = deleteMin right
                                       in Node left m right'

Од елемената дрвета можемо формирати листу. Ако прво покупимо елементе из левог поддрвета, затим корен, па затим елементе из десног поддрвета, захваљујући уређености дрвета добијена листа ће бити сортирана. На тај начин добијамо још један алгоритам сортирања (енг. tree sort).

listOfTree :: Tree -> [Int]
listOfTree Empty = []
listOfTree (Node left root right) =
   listOfTree left ++ [root] ++ listOfTree right

treeSort :: [Int] -> [Int]
   treeSort = listOfTree . treeOfList

У дрвету које смо дефинисали налазе се увек подаци типа Int, међутим, јасно је да би се на исти начин могли чувати и подаци других типова. Могуће је дефинисати и дрво којем је тип података записаних у чвору параметар (навикли сте на овакве „генеричке“ типове у језику C# где сте користили типове попут List<int> где је тип елемената колекције задат као параметарски тип те колекције).

data Tree a =
   Empty
 | Node (Tree a) a (Tree a)
deriving Show

У овом случају тип означен са a је параметар типа дрво. Дрво садржи лево и десно поддрво (која такође имају елементе типа a) и вредност типа a.

Да бисмо могли формирати претраживачко дрво, тип a мора да подржи поређење елемената, тј. мора бити класе Ord.

insert :: Ord a => Tree a -> a -> Tree a
insert Empty x = Node Empty x Empty
insert (Node left root right) x
   | x < root  =  Node (insert left x) root right
   | x > root  =  Node left root (insert right x)
   | otherwise =  Node left root right

Ред¶

Листа једноставно може да се користи као стек. Елементи могу да се додају са почетка и скидају са почетка листе у линеарној сложености. Међутим, ред је мало компликованије имплементирати (наравно, постоје библиотечке имплементације, али ћемо га овде, вежбе ради, имплементирати ручно).

Додавање елемената на крај листе има линеарну сложеност, па ред није добро имплементирати помоћу листе. Уобичајени начин имплементације реда у функционалним језицима је тзв. амортизовани ред (енг. amortized queue) који се састоји од две листе.

data Queue a = Queue [a] [a]

У празном реду су обе листе празне.

emptyQueue :: Queue a
emptyQueue = Queue [] []

Елементи се увек додају на почетак прве листе, а скидају са почетка друге.

Операцију додавања елемента у ред је тривијално имплементирати.

push :: a -> Queue a -> Queue a
push x (Queue left right) = Queue (x : left) right

Уклањање елемента из реда је мало компликованије. Функцију ћемо дефинисати тако да врати уклоњени елемент и нови ред. Пошто уклањање из празног реда није могуће, потребно је да се некако у повратној вредности укључи и могућност да је враћена вредност са почетка реда, али и да уклањање није успело. Програмски језици углавном ово решавају тако што типове проширују специјалном вредношћу null која означава да операција није успешно извршена. У функционалним језицима се обично користи посебан тип Maybe који омоћава разликовање исправних и недостајућих вредности.

Тип Maybe a омогућава представљање опционих вредности типа a. Конструктор Nothing означава недостајућу вредност, а Just нормалну вредност. На пример, Just 3 је податак типа Maybe Int. Овај тип се често користи да означи повратне вредности функција које из неког разлога некада не могу да врате исправну вредност. На пример, ако функција успе и треба да врати вредност 3, она ће вратити вредност Just 3, а ако не успе, вратиће вредност Nothing (ово одговара вредности null у програмском језику C#, која служи да означи недостатак исправне вредности).

Предност коришћења посебног у односу на специјалну вредност null је то што је једини начин да се до исправне вредности дође тај да се експлицитно испита да ли је вредност исправна. Ово се обично имплементира или поклапањем шаблона или изразом case.

g x = case f x of
         Nothing -> -1
         Just value -> value

Пошто није могуће скидање вредности из празног реда, Уместо да функција pop враћа пар типа (a, Queue a), она ће враћати пар типа (Maybe a, Queue a).

Aко је цео ред празан, наша функција pop враћа Nothing и празан ред. Ако десна листа није празна, враћамо њен први елемент (упакован у конструктор Just), док ред мењамо тако да му лева листа остаје неизмењена, а десна скраћена за њен почетни елемент. Ако је само десна листа празна, тада обрћемо леву листу и пребацујемо је на десну страну и затим уклањамо први елемент тако добијене листе.

pop :: Queue a -> (Maybe a, Queue a)
pop (Queue [] []) = (Nothing, Queue [] [])
pop (Queue left (x:xs)) = (Just x, Queue left xs)
pop (Queue left []) = let x:xs = reverse left
                       in (Just x, Queue [] xs)

Сложеност најгорег случаја операције pop је линеарна, јер је функција reverse линеарне сложености. Ипак, након једног пребацивања елемената са леве на десну страну, много наредних операција pop ће бити могуће извршити веома брзо. Ако анализирамо пут сваког елемента кроз ред, видимо да ће он једном бити додат на почетак леве листе, једном бити склоњен са почетка леве и додат на почетак десне листе (ово се догађа током извршавања функције reverse) и на крају једном скинут са десне листе. Дакле, сваки елемент учествује у тачно четири операције константне сложености, па се \(n\) елемената реда може обрадити у сложености \(O(n)\), што значи да операције додавања и уклањања елемената имају константну амортизовану сложеност.

Да бисмо могли да експериментишемо са овом структуром података, пожељно је да можемо да је испишемо. Аутоматски генерисана функција исписа (коју можемо добити ако након дефиниције типа ставимо deriving Show) приказује интерну репрезентацију података тј. садржај обе листе.

Ако желимо да прикажемо садржај елемената реда у једној листи (дакле, онако како га замишљамо, а не како је имплементиран), можемо дефинисати своју функцију приказа у облику ниске карактера. То можемо урадити на следећи начин.

show :: Queue a -> String
show (Queue left right) = show (right ++ reverse left)

Ниску добијамо тако што спојимо десну и обрнуту леву листу (тиме је елемент који је први на реду за скидање приказан на почетку). Приметите да ту листу претварамо у ниску позивом функције show, међутим, ово није рекурзивни позив јер је позвана функција show другог типа (она претвара листу, а не ред у ниску карактера).

Претходна функција show се користи када је корисник експлицитно позове, али неће бити позивана аутоматски када год је потребно да се неки ред прикаже на екрану. Да би се то постигло, морамо да користимо механизам класа типова тј. да нагласимо да наш тип Queue припада класи типова Show, при чему се за приказ не користи аутоматски генерисана функција (добијена клаузулом deriving Show), већ специфична функција коју ми дефинишемо. Да би се то урадило, користи се клаузула instance.

instance Show a => Show (Queue a) where
   show :: Queue a -> String
   show (Queue left right) = show (right ++ reverse left)

Овим смо рекли да тип Queue a припада класи типова Show тј. може да се прикаже (део Show (Queue a)), међутим, то важи само под условом да тип а припада класи Show тј. може да се прикаже (део Show a =>). Затим дефинишемо функцију show која дати ред представља у облику ниске карактера.

Вежба – алгебарски типови података¶

Као вежбу алгебарских типова података имплементирајмо структуру података речник.

Дефинисати тип података за представљање речника (мапе) елемената типа k у елементе типа v. Речник треба да буде реализован помоћу уређеног бинарног дрвета.

data Map k v =  Null
              | Node k v (Map k v) (Map k v)
              deriving Show

Дефинисати функцију која проверава да ли је речник празан.

empty :: Map k v -> Bool
empty Null = True
empty _    = False

Дефинисати функције за уметање тј. ажурирање вредности у речнику.

• Дефинисати прво функцију insertWithKey која датом кључу придружује дату вредност ако тај кључ већ не постоји у речнику, а ако постоји онда му придружује нову вредност применом задате функције на тај кључ, стару вредност и нову вредност.

• Коришћењем претходне функције дефинисати затим функцију insert, која датом кључу придружује дату вредност (ако кључ већ постоји у речнику, стара вредност се занемарује).

insertWithKey :: Ord k => (k -> v -> v -> v) -> k -> v -> Map k v -> Map k v
insertWithKey f k v Null = Node k v Null Null
insertWithKey f k v (Node k' v' l r)
  | k < k'   = Node k' v' (insertWithKey f k v l) r
  | k > k'   = Node k' v' l (insertWithKey f k v r)
  | k == k'  = Node k' (f k v' v) l r

insert :: Ord k => k -> v -> Map k v -> Map k v
insert = insertWith (\ v v' -> v')

Дефинисати функцију која листу парова (кључ, вредност) претвара у речник.

fromList :: Ord k => [(k, v)] -> Map k v
fromList = foldl (\m (k, v) -> insert k v m) Null

Дефинисати функцију find, која проналази вредност придружену датом кључу у речнику. Резултат треба да буде типа Maybe v, што значи да треба да буде Nothing ако кључ не постоји у речнику, односно Just v ako je кључу придружена вредност v.

Коришћењем функције find дефинисати функцију findWithDefault, која враћа вредност придружену датом кључу или задату подразумевану вредност ако кључ не постоји у речнику.

Коришћењем функције find дефинисати функцију containsKey, која за дату мапу враћа функцију која проверава да ли кључ постоји у речнику.

find :: Ord k => Map k v -> k -> Maybe v
find Null _ = Nothing
find (Node k v l r) k'
  | k' < k  = find l k'
  | k' > k  = find r k'
  | k' == k = Just v

findWithDefault :: Ord k => v -> k -> Map k v -> v
findWithDefault dflt k m = case find m k of Nothing -> dflt
                                            Just v -> v

containsKey :: Ord k => Map k v -> (k -> Bool)
containsKey m k = case search m k of Nothing -> False
                                     Just _ -> True

Дефинисати функцију adjustWithKey која мења вредност датом кључу тако што нову вредност одређује применом дате функције на кључ и стару вредност.

adjustWithKey :: Ord k => (k -> v -> v) -> k -> Map k v -> Map k v
adjustWithKey f k Null = Null
adjustWithKey f k (Node k' v' l r)
  | k < k'   = Node k' v' (adjustWithKey f k l) r
  | k > k'   = Node k' v' l (adjustWithKey f k r)
  | k == k'  = Node k' (f k v') l r

Дефинисати функцију која уклања најмањи кључ из речника.

Дефинисати затим функцију која уклања дати кључ из речника.

deleteMin :: Map k v -> ((k, v), Map k v)
deleteMin (Node k v Null r) = ((k, v), r)
deleteMin (Node k v l r) = let ((k', v'), d) = deleteMin l
                            in ((k', v'), Node k v d r)

delete :: Ord k => k -> Map k v -> Map k v
delete k Null = Null
delete k (Node k' v' l r)
 | k < k'  = Node k' v' (delete k l) r
 | k > k'  = Node k' v' l (delete k r)
 | k == k' = case r of Null -> l
                       _    -> let ((k', v'), d) = deleteMin r
                                in Node k' v' l d

Дефинисати функционал fold за речник. Он као први аргумент прима функцију која на основу претходног резултата, кључа и вредности придружене кључу ажурира резултат, као други аргумент прима почетну вредност резултата, а као трећи аргумент прима речник.

Коришћењем тако дефинисаног функционала fold дефинисати функцију size, која израчунава величину речника (број кључева у речнику), затим функцију toList, која креира листу парова (кључ, вредност) из речника, сортирану по кључевима и на крају функцију union која прави унију два речника (ако кључ постоји у оба речника потребно је придружити му вредност из другог).

foldMap :: (a -> k -> v -> a) -> a -> Map k v -> a
foldMap _ i Null = i
foldMap f i (Node k v l r) =
  foldlMap f (f (foldlMap f i l) k v) r

size :: Map k v -> Int
size = foldMap (\ a k v -> a + 1) 0

toList :: Ord k => Map k v -> [(k, v)]
toList = reverse . foldlMap (\ a k v -> (k, v) : a) []

union :: Ord k => Map k v -> Map k v -> Map k v
union m1 m2 = foldlMap (\ a k v -> insert k v a) m1 m2