Линеарна регресија¶

Вратимо се сада на пример који смо користили за упознавање парадигме програмирања вођеног подацима. У скупу података имали смо информације о квадратури некретнина и њиховим ценама, а наш задатак је био да научимо везу између ових вредности тако да можемо да процењујемо цене за нове некретнине.

Једноставности ради, нека буде да располажемо скупом за тренирање који садржи 10 инстанци које су пописане у доњој табели:

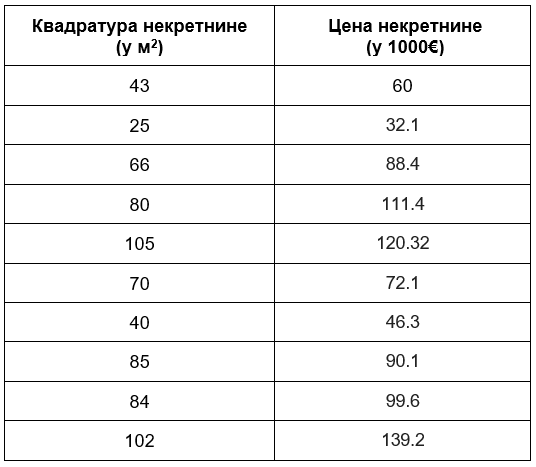
Ове инстанце можемо да прикажемо и графички. Дуж x-осе ћемо поставити вредности квадратура, дуж у-осе вредности цена некретнина и парове вредности обележити плавим кружићима.

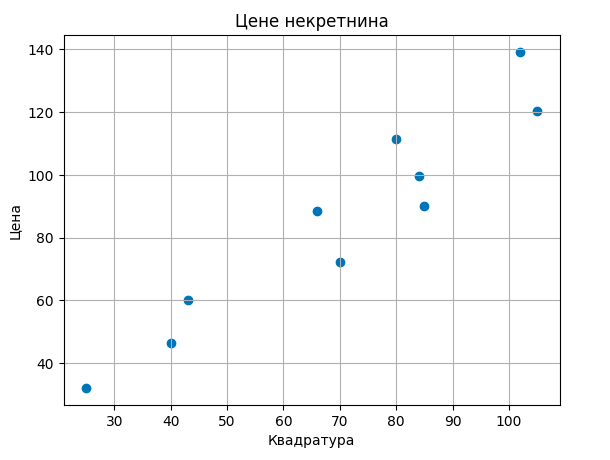
Одаберимо за модел функцију која повезује квадратуре некретнина \(x\) и цене некретнина \(y\) једначином \(y = \beta_0 + \beta_1x\), где \(\beta_0\) и \(\beta_1\) представљају непознате параметре. Ово је такозвани линеарни модел, а пошто га користимо за решавање задатка регресије зовемо га и моделом линеарне регресије. Приметимо да је ово заправо једначина праве \(y = kx + n\), где је коефицијент правца праве обележен са \(\beta_1\) а слободни члан са \(\beta_0\). Мотивација за увођење овог модела лежи у томе што тачке прате замишљену дијагоналу квадранта, можда мало спуштену ниже.

Ова секција је упарена са Jupyter свеском 06-linearna_regresija.ipynb. Да би могао да пратиш садржај даље, кликни на линк, а потом и на дугме да би се садржај отворио у окружењу Google Colab. Уколико свеске прегледаш на локалној машини, међу садржајима пронађи свеску са истим именом и покрени је. За детаљније инструкције погледај секцију Hands-on зона и лекцију Jupyter свеске за вежбу.

Твој задатак је да у пратећој свесци учиташ скуп података о некретнинама и да одабереш вредности параметара \(\beta_0\) и \(\beta_1\) за које мислиш да најбоље одговарају овим подацима. Можеш их фино подешавати померањем слајдера лево и десно. Запамти вредности које си одабрао и које идеје су те водиле приликом одређивања параметара.

Вероватно си се трудио да приликом избора параметара добијеш праву која прилази што ближе задатим тачкама и прави што мања одступања. Појединим изборима параметара си био подједнако задовољан док су неки били баш лоши. И из угла машинског учења покушавамо да пронађемо вредности параметара \(\beta_0\) и \(\beta_1\) за које правимо најмању грешку с тим што морамо прецизно да дефинишемо шта је то заправо грешка. Ево како ћемо то урадити.

Претпоставимо да су одабране вредности \(\beta_0=6,3\) и \(\beta_1=1,02\). Проширимо сада табелу са подацима колоном са вредностима које је израчунао овај модел линеарне регресије за вредности квадратура којима располажемо. Њих из угла модела представљамо величином \(x\).

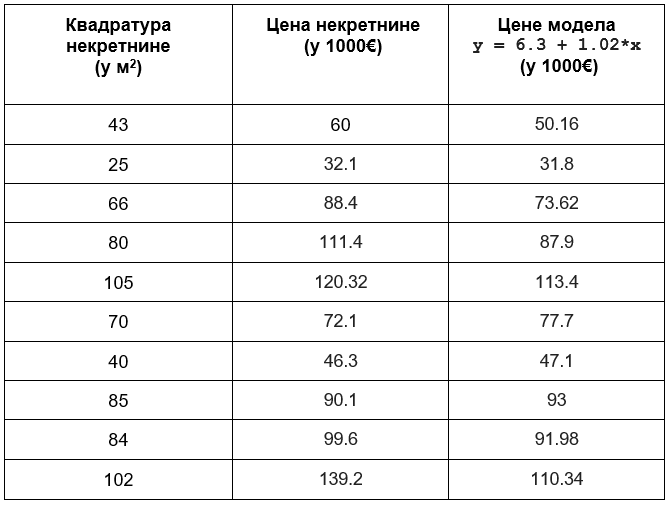
Разлика вредности које су очекиване (познате у скупу података) и вредности које смо израчунали (не заборави да њих зовемо предикцијама) представља грешку. Израчунајмо сада све грешке и забележимо их у табели.

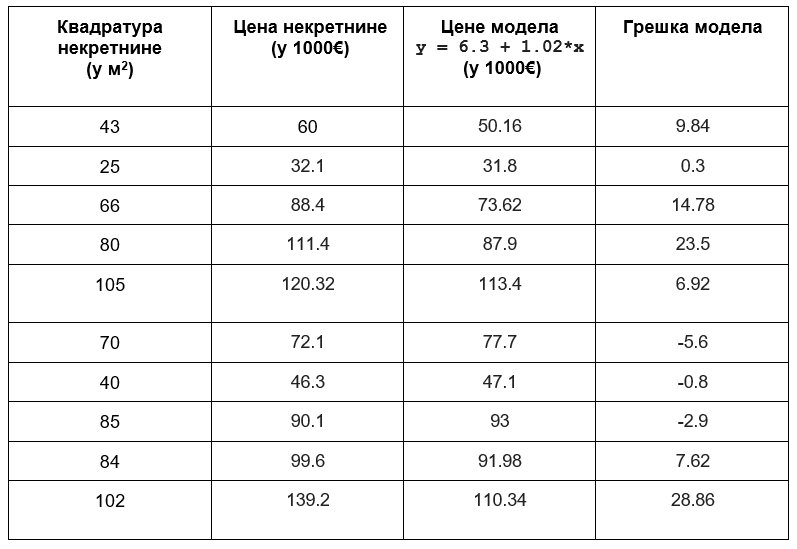
Да би лакше могли да испратимо понашање грешака, на доњој слици су њихове вредности приказане плавим испрекиданим линијама.

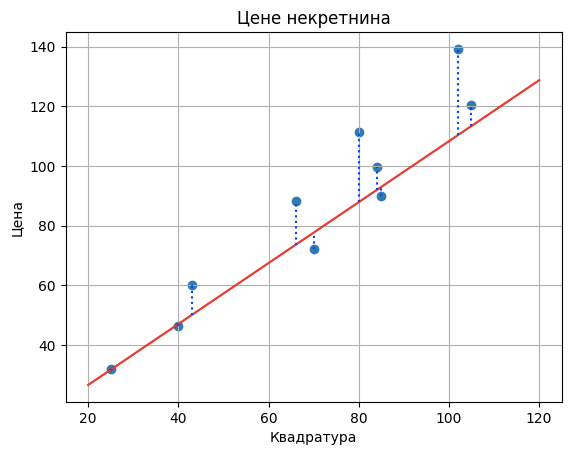
Да бисмо добили представу о укупној грешци модела, није мудро сабирати појединачне грешке пошто су неке вредности грешака позитивне а неке вредности негативне. Зато можемо да их квадрирамо па саберемо - ово ће нам пренети и јачу информацију о величини грешке без обзира на то да ли је позитивна или негативна. Уколико овако добијени збир поделимо бројем инстанци у скупу, добићемо представу о просечној грешци модела. У нашем случају то је: (9,84² + 0,32² + 14,782² + 23,52² + 6,92² + (-5,6)² + (-0,8)² + (-2,9)² + 7,62² + 28,86²)/10 = 184,687

Овако израчуната грешка модела линеарне регресије се зове средњеквадратна грешка (енг. mean squared error, MSE). За фиксиране вредности параметара \(\beta_0\) и \(\beta_1\) поступак израчунавања који смо описали можемо скраћено приказати формулом \(\frac{1}{n}\sum_{i=1}^n{(y_i - (\beta_0 + \beta_1x_i))^2}\). У њој парови \((x_i, y_i)\) одговарају појединачним инстанцама, квадратурама некретнина \(x_i\) и њиховим ценама \(y_i\), а бројем \(n\) je означен укупан број инстанци. То је 10 у нашем случају. Израз који фигурише у суми представља разлику очекиваних \(y_i\) и израчунатих \(\beta_0 + \beta_1x_i\) вредности.

Средњеквадратна грешка је грешка коју увек упарујемо са моделом линеарне регресије и коју желимо да што више смањимо избором правиx параметара \(\beta_0\) и \(\beta_1\). Из искуства подешавања параметара си видео да то и није баш лак задатак. Срећом, постоје математичке технике које нам у томе могу помоћи. Да бисмо открили како ово да урадимо, пређимо на следећу лекцију о градијентном спусту.