Регуларизација¶

Регуларизације представљају још једaн скуп техника које се могу користити за контролу преприлагођавања модела. Њихов основи циљ je да спрече комплексне моделе, који нам помажу да научимо богатији скуп зависности у подацима, да се превише прилагоде.

Регуларизацију ћемо увести на примеру модела линеарне регресије. Претпоставимо да смо обучили модел и да смо добили вредности параметара чији графички приказ изгледа као на слици.

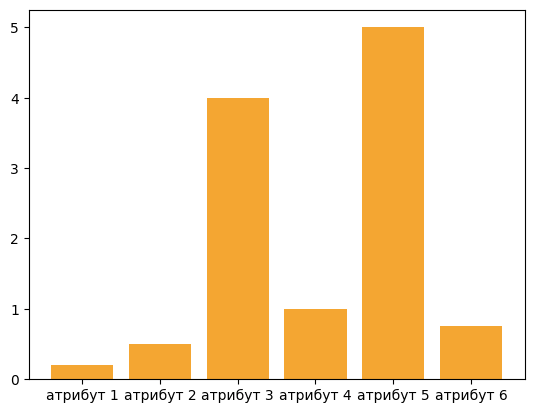
Параметри који су по својој (апсолутној) вредности највећи су уједно и најзначајнији за предикције модела. На слици су то параметри који одговарају атрибутима 3 и 5 и њихове вредности су, као што можемо да приметимо, знатно веће од вредности преосталих параметара. У том смислу, ови атрибути могу да занемаре утицај преосталих атрибута на вредности предикција па ово понашање модела можемо да протумачимо и као вид преприлагођавања подацима.

Зато је пожељно, у некој мери, ограничити вредности параметара - желимо да модел научи параметре и да они осликавају својства података, али желимо и да пратимо њихову вредност како би предупредили преприлагођавање. Ова техника се зове регуларизација (енг. regularisation). У контексту линеарне регресије то можемо урадити додавањем суме квадрата параметара средњеквадратној грешци модела: \(\frac{1}{N}\sum_{i=1}^N{(y_i - (\beta_0 + \beta_1x_i + \beta_2x_2 + ... + \beta_nx_n))^2} + \lambda(\beta_1^2 + \beta_2^2 + ... + \beta_n^2)\). Вредност \(λ\) која фигурише у изразу је хиперпараметар којим утичемо на јачину регуларизације. Ако је његова вредност 0, регуларизација неће имати никаквог ефекта. Задавањем неких не-нула вредности балансирамо учење одређено средњеквадратном грешком и преприлагођавање мерено вредностима суме квадрата параметара. Квадрати су ту из техничких разлога, прво да би онемогућили да се вредности коефицијената између себе потиру, а потом и да би се очувала својства функције грешке за примену алгоритма оптимизације. Овако проширени облик линеарне регресије допуњен регуларизационим чланом назива се гребена линеарна регресија (енг. ridge regression).

Нешто касније ћемо се вратити на причу о регуларизацији када будемо увели неуронске мреже. Оне су веома комплексни модели па се често могу преприлагодити подацима. Видећемо и како то можемо да пратимо.