Одређивање броја кластера¶

Број кластера k=4 у претходном примеру није сасвим случајно изабран, има везе са начином на који смо генерисали скуп података (можда си то и приметио у функцији kreiraj_podatke која нам је помогла око овог задатка). Када радимо са реалним скуповима података са више инстанци и атрибута, није баш интуитивно претпоставити колико кластера треба издвојити. Зато нам је потребан неки прецизнији начин одређивања најбоље вредности за број k.

У теорији машинског учења је познато да задатак разбијања скупа података у k кластера на начин који смо описали одговара проналажењу најмање вредности функције чија је формула приказана ниже. Иза ове наизглед компликоване суме крије се једноставна идеја: очекивање да свака инстанца буде што ближе центроиди свог кластера. Зато се за све инстанце кластера прати колико су удаљене од своје центроиде (прва сума) а затим се те вредности саберу за све кластере (друга сума).

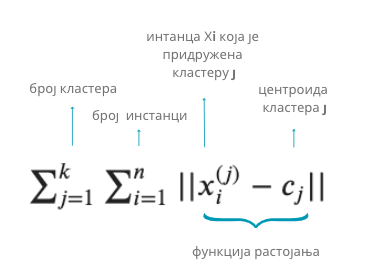
Функција грешке алгоритма к-средина

Оптималан број кластера k одређујемо тако што пратимо понашање алгоритма за различите вредности параметра k. Ако бисмо за скуп података из претходног примера испробали вредности броја k од 1 до 10 и приказали вредности ове функције грешке графички, добили бисмо график као на доњој слици.

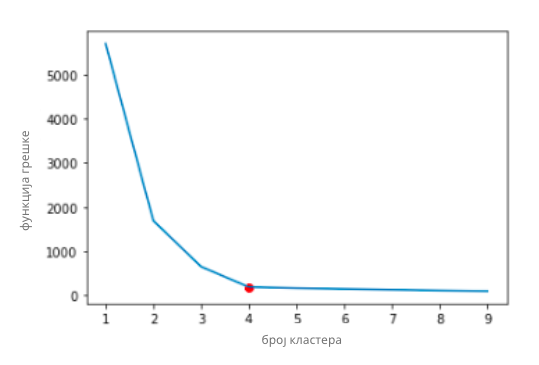
График функције грешке

Екстремни случајеви кластеровања (и неупотребљиви у пракси) су да све инстанце буду у једном кластеру и да свака инстанца буде у свом кластеру. Када су све инстанце у једном кластеру, грешка је највећа, а када број кластера одговара броју инстанци, вредност функције грешке је нула. Зато приликом претраге оптималног броја k треба да се позиционирамо негде између, где је и број кластера задовољавајући и где је грешка довољно мала. На графику је та тачка приказана црвеном бојом и одговара вредности параметра k=4. За веће вредности броја k вредности грешке су сличне, док су за мање вредности броја k вредности грешке непожељније. Овакве тачке се обично виде у форми ”лакта” на графику овог типа па се цео метод одређивања оптималне вредности зове метода лакта (енг. elbow method).

С обзиром на функцију грешке која прати кластеровање алгоритмом к-средина, кластери који се на овај начин проналазе су сферични и осетљиви на присуство одударајућих података.